Science Concepts: torque, angular velocity, rotational inertia
In a previous article, I talked about the importance of velocity over mass when dealing damage with strikes. What I didn’t say was how you go about doing that. So that’s what I’m going to cover now, at least for circular/curving strikes. This could be a hook punch, a round kick, a back fist, a stick swing, or any other kind of strike that involves curving motion.
The Science
In my last article, I covered angular velocity. Generating a fast, curving strike is done by applying torque to generate circular motion at multiple parts of your body. In fact, generating power in all sorts of athletic contexts is done this way. It’s the way a quarterback throws a football or the way a baseball player swings a bat. It’s the way a hockey player shoots a puck or the way a gymnast tumbles through the air. Many small instances of circular motion combined, with the right timing, generate incredible speed and power.
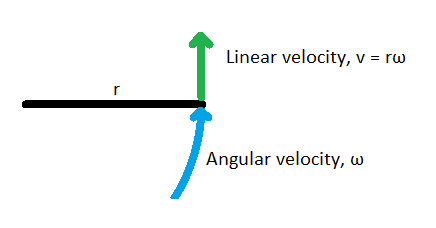
Consider this basic example:
This is essentially what happens when you move one of your joints. However fast your muscles that cause the movement can go is the limit of the angular and linear velocity. But what if the center of the circle was also moving? We could achieve that with a situation like this:
The first part swings the second part, which still has the same angular velocity as before, relative to its own center. However, the center of the second part now has its own angular and linear velocity, adding to the velocity of the tip.
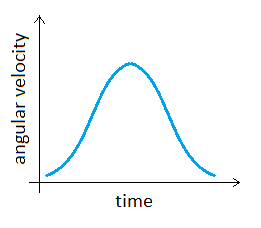
Also keep in mind that each swinging motion has a beginning, middle, and end at which the speed is increasing, maximum, and decreasing, respectively.
Conceptually, this is enough to apply. Mathematically, we would find the angular acceleration of each swinging piece and find where it changes from positive to negative to determine the point at which the angular velocity is maximum. Yay calculus.
Another important concept for curving strikes is rotational inertia. Rotational inertia is a property of an object to resist a spinning motion. The exact calculation of this property depends on the density of the object, the shape of the object, and the direction of rotation. Wikipedia has an excellent entry on it here. To see how rotational inertia relates to regular inertia (which is just measured by mass), let’s look at the formula for kinetic energy.
So, you can see that the third line is structured like the first accept that we have? (angular velocity) instead of v (linear velocity) and mr2 (rotational inertia) intsead of m (linear inertia). Now, this is true for a point mass, but for more complex objects you need to get an average (usually via an integral) but on to the point.
Since the formula above involves the radius of the rotating object and since energy cannot be created or destroyed (one of those physic laws that is never violated, ever), if we change the radius by moving a limb in towards the center or out away from it, the angular velocity must change as well in order to keep the energy the same. The typical example of this is when a figure skater spins and pulls her limbs in to start spinning faster. She didn’t create energy. She just shifted the source of the energy from the radius to the angular velocity.
We can use this idea for curving strikes as well. This shows up most easily in hook punches, hook kicks, and swinging stick strikes. If you use your muscles to get your body rotating with the limb out and then pull it in (as in for a tight hook punch) then the velocity will increase (every little bit helps). Remember: velocity has a bigger impact of the damage you do than the mass behind the strike.
You can also use rotational inertia in the other direction, with some good timing to help get a strike up to speed with less energy than staying at full extension. By staying tight to your body (think, back spin kick), you can rotate very quickly and easily. Once your speed is up and you’re coming around to your target, extend your limb at the last moment (no pun intended) to get the best (ish) of both worlds. Because you extend your limb just prior to impact, the extra rotational inertia doesn’t have much time to slow down your motion. So you can the speed from a tight spin with full extension. Keep in mind that your timing has to be excellent for this to work. Otherwise, your extension will just cause your strike to slow down and reduce the damaging effects.
The Application
What does this mean for techniques? It means that getting multiple joints of your body engaged in a motion so that they are all moving in the same direction, for a moment, is the way to maximize your speed (and therefore kinetic energy). For a round kick your quadriceps swing your shin, your hip flexors swing your upper leg, your torso swings your hips, and your supporting leg pivots your torso. When all of these motions work together so that the maximum speed of each motion coincides, the result is a very fast and powerful kick. Combine that with a well timed extension, using rotational inertia, and you’re going to be kicking very hard indeed.
Just apply these concepts to any rotating motion to achieve optimal speed at an instant of time.
Conclusion
Curving attacks are just like any other athletic movement. You have to get your whole body working together with the right timing. That’s what coaches all over the world will tell you. Scientifically, they’re saying that you need the angular velocity of each joint in your body to coincide in time to match up at their highest points to achieve that ultimate result of a speedy…whatever it is you’re doing. By using the concept of rotational inertia, you can provide a mechanical advantage to achieve even higher speeds. Think through your techniques and really analyze the motion of each joint of your body as you go through those techniques. When you get the timing right, the end result can be quite impressive.