Science concepts: angular velocity, linear velocity
In the classes I teach, I almost always have the students do knife sparring as part of the warm up. I make it into a bit of a game where getting cut in various target zones requires you to do certain exercises (to de-incentivize bad habits). It’s easy to tell who has been with us for a while and who is new by watching who is doing the most exercises.
One of the pit falls that untrained people seem to get into is watching the knife too closely. Now, I’m not advocating that you don’t keep track of the knife. In a real situation, that’s the thing that’ll kill you. So, you should definitely track it, but I recommend that people watch the elbow (and the forearm to an extent) rather than the knife. Invariably, when I tell people to do this, they see immediate improvement. Why? Because of the difference between angular velocity and linear velocity.
Definitions
Linear velocity is the easy one. That’s simply how much distance is covered per unit of time. I covered this way back in the
physics primer. Angular velocity is a bit different. It’s all about circles. It is the portion of a circle swept out per unit of time. This is often depicted uses a unit of radians per second. Radians are a bit weird. They’re a unit…but not. There are 2π radians in a circle (just like 360 degrees covers a circle). So, 180 degrees is equivalent to 1π. If a wheel rotates all the way around two times per second, then the angular velocity would be 4π rad/s.
To find the linear equivalent of an angular velocity you need to know the radius of the circle being swept out. Once you know that the conversion is easy. Just take the angular velocity, ω (angular velocity…and acceleration…and angles are often depicted using Greek letters, this isn’t a ‘w’ it’s a lower-case omega) and multiply it by the radius r to get the linear velocity, v.
v = rω
Simple enough.
The Science
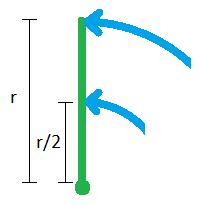
Like I’ve said before, joints allow for circular motion. In the case of a slashing knife or a hooking punch, the shoulder is effectively the center of the circle. The elbow is about halfway out and the hand is on the outer edge of the circle. Let’s look at a generic example:
The picture could represent a swinging stick. Though I’m just using it to illustrate the basics here. Since the stick is rotating about one end, each part of the stick has the exact same angular velocity, ω. The same number of radians are being swept out per second. However, the linear velocity of each point is different based on how far from the center of rotation it is. Here, the end point has a velocity of rω, but the midpoint has a velocity of (r/2)ω. That’s half the velocity.
When trying to track motion with your eyes, slower is easier. The less degrees of freedom the thing your eyes are tracking has, the easier it’ll be to keep up. This is why watching the elbow is easier than watching the hand. The nice thing about watching the elbow is that it’ll reveal the direction from which the hand will strike you. So, you don’t lose any information and it’s easier to obtain. Win-win.
Applications
The applications of this principle are many and varied. At my dojo, we teach watching the elbow as part of our essential knife defense for beginners. When dealing with punches, we watch the elbows to increase effectiveness in capturing the extended arm. When stick fighting, watching the forearm and hand is way easier than trying to track the tip of the stick, which can move at ridiculous speeds (scientifically, “ridiculous” speeds are somewhere near “plaid”). As a former Taekwondo guy, I can say that watching the knee is easier than watching the foot and provides just as much information about where the attack is coming from. One time I landed a kick on a guy’s nose using some TKD trickery. My success was only there because he watched my foot rather than my knee (probably…given that he was better than me). The list goes on.
Conclusion
Angular velocity is a relatively simple and low-level principle, which is why is applies to so many areas of fighting. Understanding angular velocity and how it is different from linear velocity will help you to understand why many techniques are taught they way they are. Also, getting a firm grasp on angular velocity (and angular movement) will be required for understanding slightly more complicated things like rotational inertia and how it relates to energy…but that’s for another time!